L'unione della pedaliera alla tastiera

Come ho già avuto modo di illustrare nel post dello scorso 6 Ottobre, nel mio organo a canne la pedaliera non comanda un corpo d'organo proprio ma si limita ad azionare il corrispondente tasto del manuale (cioè della tastiera).

Tale funzione di unione è svolta da un dispositivo meccanico che deve trasmettere il movimento di ogni tasto della pedaliera a quello del corrispondente tasto della tastiera.

Visto che:

      1) la corsa (escursione verticale) dei tasti della pedaliera è maggiore di quella dei tasti della tastiera

      2) la distanza tra due tasti contigui è più alta nel pedale, rispetto al manuale

non è possibile realizzare l'unione tramite dei semplici fili; serve un sistema composto da tiranti e catenacci denominato catenacciatura di riduzione o più semplicemente catenacciatura.

Anche nel caso del collegamento tra la tastiera e il somiere si presenta lo stesso problema, che infatti viene risolto con una catenacciatura appositamente costruita (lo vedremo più avanti).

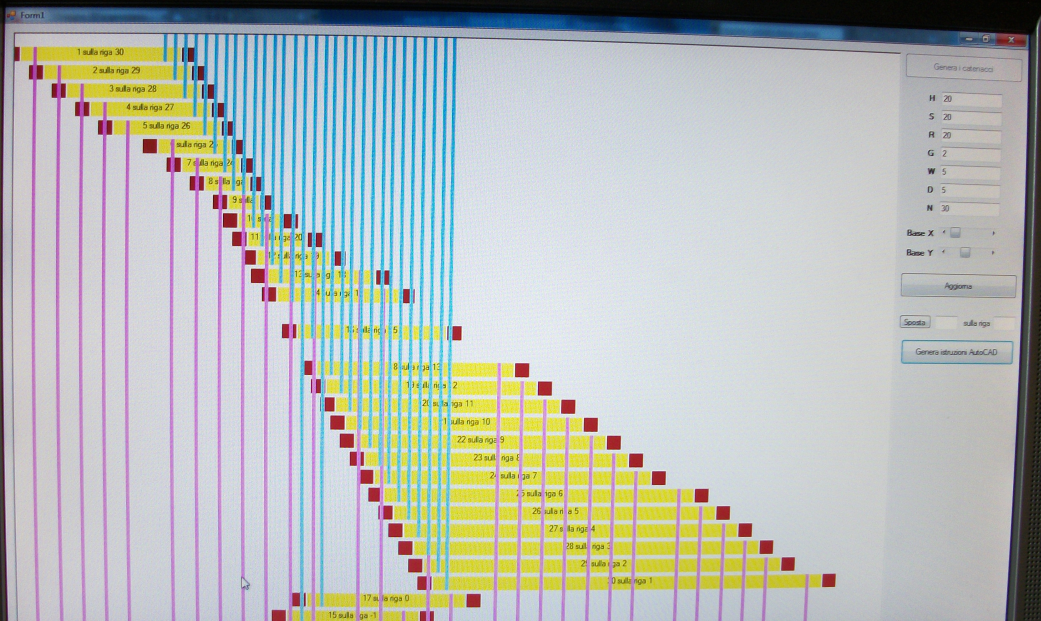
Per la progettazione della catenacciatura di unione del tasto al pedale mi sono avvalso del programma AutoCAD (versione per studenti) e di un programma, scritto da me in Visual Basic nel 2011, che ho denominato Wellenbrett (traduzione del termine tecnico catenaccio in lingua tedesca).

I dati relativi alle posizioni dei tasti del manuale e del pedale devono essere inseriti in un file "elenco.txt" che viene successivamente caricato da Wellenbrett all'avvio.

AGGIORNAMENTO Metto a disposizione degli interessati un file ZIP contenente il software, il suo codice sorgente e le note di programmazione. Se qualcuno poi volesse modificarlo per apportare delle migliorie, segnalare degli errori o magari renderlo multipiattaforma, è il benvenuto: potete contattarmi ad esempio tramite la mia pagina Facebook Omnia Vincit Musica.

Il programma legge i dati e genera una schermata grafica della catenacciatura: a questo punto è possibile modificare tale schema iniziale di collegamento spostando, a proprio piacimento, in alto o in basso ogni singolo catenaccio con l'apposito comando "sposta" posto alla destra della schermata, fino ad arrivare ad una situazione ottimale nella quale non sussistono più sovrapposizioni tra i tiranti verticali (tali sovrapposizioni genererebbero problemi in fase costruttiva).

Cliccando poi "genera istruzioni AutoCAD" il software genera un set di istruzioni che possono essere ricopiate direttamente nella linea di comando del programma CAD in modo da disegnare automaticamente le varie parti meccaniche che compongono il sistema.

Una possibile evoluzione futura del programma è quella che consente di evitare il riposizionamento manuale dei catenacci, applicando qualche sorta di algoritmo topologico scritto appositamente.

Torniamo quindi all'aspetto costruttivo vero e proprio: la tavola che supporta la catenacciatura è stata ricavata da un pannello rettangolare multistrato in legno di pioppo successivamente sagomato a forma di trapezio (allo scopo di alleggerirne il peso eliminando le zone non necessarie).

Per costruire i catenacci ho acquistato dei lunghi parallelepipedi a sezione quadrata in legno di abete (già piallati) tagliandoli alla lunghezza adeguata, stessa strategia utilizzata anche per la costruzione dei tiranti che però sono in legno di koto e hanno sezione rettangolare, così come le levette dei bilancieri. Per collegare le estremità dei tiranti ai tasti del manuale e del pedale e alle levette dei catenacci ho usato del filo di ferro dolce.

Ogni catenaccio è sostenuto da due supporti laterali in legno di mogano sapelli nei quali sono inseriti due chiodini di ferro.

Per ovviare al problema del punto 1, ovvero la differenza di corsa tra il pedale e il manuale, ho dovuto costruire un ulteriore dispositivo di riduzione (realizzato in koto e in pino) che riduce il movimento verticale generato dai tasti della pedaliera prima di trasmetterlo a quelli del manuale: di seguito propongo alcune foto della sua costruzione.

Qui di seguito si può ammirare il risultato finale: la catenacciatura di unione tasto al pedale collegata alla tastiera e al meccanismo di riduzione dell'escursione dei tasti della pedaliera.

In quest'ultima foto si può vedere, oltre alla catenacciatura di unione pedale-manuale, anche quella che collega la tastiera al somiere:

Il rifornimento d'aria nell'organo a canne

Durante il suo utilizzo l'organo a canne consuma una certa quantità di aria in pressione: tale consumo varia in continuazione durante l'esecuzione dei brani, in funzione del numero di tasti premuti e del numero di registri inseriti in un determinato momento.

Affinché la frequenza dell'onda acustica emessa da ogni canna rimanga costante nel tempo è assolutamente necessario che la pressione dell'aria all'interno dello strumento non subisca variazioni significative, né durante una sessione di utilizzo, né tantomeno nel corso degli anni.

Generalmente i valori di pressione di un organo a canne, che vengono fissati in fase di costruzione, oscillano tra i 45 e i 90 mmH₂O (millimetri in colonna d'acqua): molto però dipende dallo stile costruttivo scelto dall'organaro e dalle tradizioni che variano a seconda del luogo: ad esempio gli organi a canne di fabbricazione tedesca utilizzano generalmente pressioni di esercizio più elevate rispetto a quelli di fabbricazione italiana.

La pressione viene espressa in millimetri in colonna d'acqua perché lo strumento con il quale viene misurata è un tubo manometrico a U che viene riempito con una certa quantità di acqua, preferibilmente colorata per una più facile leggibilità del valore sulla scala.

Quello che vedete qui sotto è il tubo manometrico che ho costruito personalmente: il tubo è in plastica trasparente e l'acqua è stata colorata con un po' di inchiostro ciano (quello per stampanti ink-jet).

Una delle due estremità del tubo viene collegata al somiere dell'organo mentre l'altra estremità è libera. Quando lo strumento entra in pressione si crea un dislivello tra i due rami del tubo a U: la misura di tale dislivello, misurata ed espressa in millimetri, corrisponde alla (sovra)pressione raggiunta nel somiere.

 

L'organo a canne necessita pertanto di un sistema di rifornimento di aria a pressione costante e portata variabile: negli organi moderni questo sistema viene realizzato accoppiando un elettroventilatore ad un mantice stabilizzatore.

L'elettroventilatore deve essere "sovradimensionato" rispetto alle reali esigenze dell'organo: dovrebbe in teoria essere in grado di fornire una portata d'aria sufficiente a far suonare tutte le canne dello strumento contemporaneamente, alla pressione di esercizio fissata in fase di costruzione.

Il mantice stabilizzatore di pressione può essere costruito a cuneo, a lanterna o a vasca: io ho scelto la seconda opzione perché è quella consigliata da alcuni testi di arte organaria.

La base del mantice è stata costruita con tavole di legno lamellare di abete spesse 18 mm mentre le stecche tagliate ad angolo sono state realizzate con legno di multistrato di pioppo spesso 5 mm i cui bordi sono stati adeguatamente smussati con la sega circolare inclinabile. La tavola superiore, flottante, e' stata realizzata con multistrato in legno di pioppo di spessore adeguato. La tenuta d'aria è assicurata da pelle incollata al legno con colla vinilica.

Sopra al mantice vengono posizionate delle zavorre (mattoni, blocchi di metallo, ecc...) il cui peso totale, unito a quello della tavola superiore del mantice, determinerà la pressione di esercizio dello strumento: io ho utilizzato un set di dischi in ghisa (quelli che si utilizzano in palestra per fare sollevamento pesi).

Affinché il sistema elettroventilatore + mantice funzioni in modo adeguato è necessario interporre tra i due elementi una apposita valvola a tendina che effettui un controllo in retroazione (feedback) sulla quantità di aria che viene immessa all'interno del mantice: la tavola del mantice è collegata con un filo di nylon al meccanismo della valvola a tendina.

Grazie a questo meccanismo più il mantice si gonfia e più a valvola a tendina viene progressivamente abbassata, diminuendo a portata d'aria in ingresso al mantice stesso.

Il foro di ingresso dell'aria nel mantice inoltre è dotato di una valvola di non ritorno che può tornare utile nel momento in cui si decidesse di alimentare l'organo a canne con un mantice ausiliario azionato meccanicamente anziché utilizzare l'elettroventilatore:

Così facendo l'aria potrà solo entrare e mai uscire dal foro di alimentazione del mantice a lanterna. Qui di seguito propongo alcune immagini relative alla costruzione e al meccanismo di funzionamento della valvola regolatrice a tendina.

Per quanto riguarda l'elettroventilatore centrifugo si deve ricordare che un dispositivo professionale per organo a canne ha un costo che può partire dai 700 euro per strumenti di piccole dimensioni fino ad arrivare a cifre molto più importanti per i grandi organi da chiesa che consumano quantità d'aria molto elevate: il costo relativamente elevato è giustificato dal fatto che tali dispositivi sono dotati di modernissimi sistemi di insonorizzazione che garantiscono una silenziosità estrema, requisito fondamentale nel caso di uno strumento musicale.

Per il mio organo a canne al momento ho optato per una soluzione di gran lunga più economica e cioè ho acquistato un soffiatore centrifugo in polipropilene da 280 W di potenza e 2850 giri al minuto che si può acquistare con meno di 100 euro: ovviamente è molto rumoroso e anche inserendolo all'interno di una cassa insonorizzante (che ho appositamente costruito) genera una certa quantità di rumore indesiderato.

I registri del mio organo a canne di legno

Nell'organo il musicista ha la possibilità di produrre varie sonorità grazie alla presenza dei registri: l'insieme dei registri costituisce la cosiddetta disposizione fonica.

Ogni organo a canne ha una propria disposizione fonica diversa da quella di altri strumenti: anche per questo motivo è corretto affermare che non troveremo mai un organo uguale ad un altro.

La disposizione fonica del mio organo a canne di legno è la seguente:

Principale 8'

Ottava 4'

Decimaquinta 2'

Decimanona 1 ⅓'

Vigesimaseconda 1'

Vacat

Si tratta quindi di un organo a canne a 5 registri che però è predisposto per montare un sesto registro aggiuntivo (vacat in latino significa vacante).

Dato che la tastiera è dotata di 54 tasti, il numero di canne totali a strumento completato sarà pari a 54 x 5 = 270 canne. Se poi decidessi di aggiungere anche il sesto registro si arriverebbe a 324.

Siamo quindi pronti per analizzare il significato del nome di ognuno dei registri presenti.

Principale 8'
Come si può facilmente intuire dal nome questo è il registro fondamentale dell'organo che fornisce la sonorità di base sulla quale è poi possibile aggiungere, durante l'esecuzione dei brani, le sonorità generate dagli altri registri. Il numero 8 si riferisce alla dimensione che la canna più lunga del registro dovrebbe avere. Ovviamente la canna più lunga è quella che genera il Do1 e cioè la 1° canna del registro, azionata dal 1° tasto della tastiera. L'apostrofo, posto alla destra del numero, indica che la misura è espressa in piedi, unità di misura di lunghezza tipica del sistema imperiale britannico.

1 piede = 12 pollici

1 pollice = 2,54 cm

quindi:

1 piede = 30,48 cm

Il registro di Principale è un registro di otto piedi ciò significa che il risuonatore del Do1 dovrebbe essere lungo all'incirca 240 centimetri.

Ottava 4'
Il registro di Ottava produce un suono che è un'ottava più in alto rispetto al registro Principale, e questo deve verificarsi per qualsiasi tasto premuto. Le canne dell'Ottava quindi hanno un'altezza dimezzata rispetto a quelle corrispondenti del registro di Principale: ecco perché si passa da otto a quattro piedi (la canna del Do1 è lunga circa 120 cm). Un modo alternativo di scrivere il nome del registro è utilizzare il corrispondente numero romano: VIII 4'.

Ad oggi l'unico registro completo e funzionante del mio organo è proprio quello di VIII 4'.

Decimaquinta 2'
Decimaquinta è un termine arcaico che in realtà significa quindicesima: ciò significa che una canna di tale registro produce, su una scala diatonica, la quindicesima nota sopra a quella base e cioè la doppia ottava. La lunghezza della canna più lunga della decimaquinta è di circa due piedi. Si può anche indicare come XV 2'.

Decimanona 1 ⅓'
Decimanona sta per diciannove e il suono che viene prodotto è la tripla quinta rispetto al suono di base del Principale. Volendo usare i numeri romani si può usare la dicitura XIX 1 ⅓'.

Vigesimaseconda 1'
Il nome di questo registro significa ventiduesima perché il suono che viene prodotto è quello della ventiduesima nota più in alto rispetto a quella generata dal registro principale, cioè la tripla ottava. L'abbreviazione in numeri romani è la seguente: XXII 1'.

Facciamo un esempio: immaginiamo di attivare in contemporanea tutti i cinque registri dell'organo e di premere il primo tasto della tastiera, cioè il Do1. L'organo produrrà cinque suoni sovrapposti (il cosiddetto ripieno) le cui corrispondenti note sono:

Do1 generato dal registro di Principale 8'

Do2 generato dal registro di Ottava 4'

Do3 generato dal registro di Decimaquinta 2'

Sol3 generato dal regitro di Decimanona 1 ⅓'

Do4 generato dal registro di Vigesimaseconda 1'

Ogni registro può essere attivato o disattivato a piacimento durante l'esecuzione dei brani musicali; ricordo inoltre che nel mio organo a canne ogni registro è diviso in due parti: la zona dei bassi e quella dei soprani.

😇 So cosa state pensando: "nell'organo a canne ci sono troppi numeri". Vi avverto: non avete ancora visto nulla... il bello deve ancora arrivare! 😀

« La musica è il piacere che la mente umana prova quando conta senza essere conscia di contare »

(cit. G.W. Von Leibniz)

La lunghezza delle canne d'organo ad anima

La formula del risuonatore di Helmholtz non è la più adatta alla determinazione della frequenza di risonanza delle canne d'organo e, di conseguenza, alla determinazione della lunghezza delle stesse. Vediamo quindi quali formule applicare nei due diversi casi delle canne d'organo ad anima: le canne aperte e le canne tappate.

Canne aperte

sezione longitudinale di una canna d'organo in legno

immagine rielaborata, tratta dal libro The Art of Organ Building di G.A. Audsley

L'equazione che segue consente di determinare la lunghezza L (in metri) del risuonatore di una canna d'organo aperta avendo a disposizione la frequenza f (Hz) che si vuole ottenere e la profondità P (m) della cavità risonante.

Canne tappate

 canna d'organo tappata, in legno
immagine tratta dal libro The Art of Organ Building di G.A. Audsley

Se invece si decide di costruire una canna tappata sulla sua estremità superiore, allora si deve applicare quest'altra formula:

Una canna tappata è in grado di generare la stessa nota musicale con un risuonatore lungo circa la metà rispetto al caso di canna aperta (lo si intuisce dal fatto che nelle rispettive formule in un caso compare un 2 a denominatore, mentre nell'altro caso compare un 4): per questo motivo a volte negli strumenti più piccoli le canne delle note più gravi vengono costruite tappate, anche se ciò comporta una discreta variazione del timbro. In questo modo si risparmia una discreta quantità di legno (o di metallo) e l'ingombro all'interno della cassa dello strumento è fortemente ridotto. Inoltre, proprio perché le canne tappate hanno un timbro diverso rispetto a quelle aperte, alcuni registri vengono appositamente costruiti con canne tappate (ad esempio il Bordone, che troviamo anche negli... orologi a cucù 🐦).

Nelle due formule che abbiamo appena visto possiamo considerare la presenza del termine sottrattivo (–2P in un caso, –P nell'altro) come un fattore correttivo che consente di correggere la lunghezza teorica del risuonatore in modo da determinare un valore piuttosto vicino a quello reale.

Nel caso di canne aperte si sottrae due volte il valore di profondità del risuonatore (–2P) perché ci sono due aperture (la bocca della canna e la sommità della canna), mentre nel caso di canne tappate si sottrare una sola volta (–P) perché il risuonatore presenta una sola apertura (solamente la bocca della canna visto che la sommità è chiusa con un tappo).

Maggiori dettagli sulla fisica acustica delle cavità risonanti possono essere trovate in questa pagina wiki.

La risonanza di Helmholtz

Secondo il principio della risonanza di Helmholtz l'aria presente all'interno di una cavità può iniziare a vibrare in modo continuo e con una frequenza ben precisa (generando quindi un'onda acustica) se viene adeguatamente eccitata.

Hermann von Helmholtz

(fisico tedesco nato nel 1821 a Potsdam, immagine tratta da Wikipedia)

Ecco qui alcuni esempi di fenomeni quotidiani in cui si può manifestare un fenomeno di risonanza di una massa d'aria presente all'interno di una cavità:

• soffiando delicatamente sul collo di una bottiglia vuota (o semi-vuota) o sull'imboccatura di una cannuccia si produce un suono che può essere un fischio nel caso di risuonatori piccoli o una nota più flautata nel caso di oggetti più grandi

• quando si riempie gradualmente una bottiglia vuota con dell'acqua ad esempio utilizzando la cannella di una fontana si può udire un "suono" che diventa sempre più acuto mano a mano che la bottiglia si riempie, fino a scomparire quando la bottiglia è completamente piena: la frequenza del suono varia, generando una nota sempre più acuta, perché via via che la bottiglia si riempie la quantità d'aria nella bottiglia diminuisce e quindi diminuiscono le dimensioni del risuonatore

• quando si sta viaggiando in automobile e tutti i finestrini sono chiusi eccetto uno che magari è aperto per metà e si verificano determinate condizioni di velocità e di pressione si può improvvisamente iniziare a udire una strana e fastidiosa oscillazione all'interno dell'abitacolo, una sorta di pulsazione che altro non è che un'onda sonora avente frequenza molto bassa (2 - 10 Hz)

In tutti questi casi si genera un'onda acustica il cui valore di frequenza di oscillazione è legato alle dimensioni, alla geometria della cavità risonante e alla modalità di eccitazione della massa d'aria.

La frequenza di risonanza di un risuonatore perfetto di Helmholtz può essere determinata con la formula seguente:

dove:   v è la velocità del suono nell'aria (m/s)

            A l'area della sezione trasversale dell'imboccatura della cavità (m²)

            L è la lunghezza dell'imboccatura della cavità (m)

            V è il volume della cavità (m³)

Costruendo una serie di oggetti cavi di varie dimensioni è quindi possibile costruire uno strumento musicale aerofono che copra tutto l'intervallo di note desiderato.

Per quanto riguarda la modalità di eccitazione della cavità risonante, nel caso delle canne d'organo ad anima è necessario che le stesse siano dotate di una struttura geometrica appositamente progettata allo scopo: questa è la bocca della canna.

La matematica delle note musicali

Come in tutti gli strumenti a tastiera la pressione di un tasto più a destra del precedente deve (generalmente) produrre un suono più acuto, mentre andando in direzione contraria (verso sinistra) si deve produrre un suono più grave.

L'acutezza (o la gravità) della nota musicale prodotta, cioè la sua altezza, può essere espressa in modo matematicamente preciso misurando la frequenza f dell'onda acustica che si propaga nell'aria.

La velocità del suono è sempre costante e pari a 343 m/s per tutte le onde sonore (in aria secca alla temperatura di 20 °C), ma la frequenza è funzione dell'altezza della nota musicale generata, e viceversa. L'unità di misura della frequenza è l'Hertz (Hz) cioè il numero di cicli al secondo compiuti dall'onda sonora in un determinato (qualsiasi) punto dello spazio in cui essa si stia propagando.

Volendo semplificare molto la questione e quindi posticipando ad una futura trattazione l'affascinante e inestricabile argomento dei temperamenti, è possibile determinare, per ogni nota musicale, la frequenza dell'onda sonora propagata.

La tastiera di un organo a canne, esattamente come quella di un pianoforte, può essere suddivisa in ottave e ogni ottava può essere numerata con un numero crescente da sinistra verso destra.

L'ottava contiene 7 note naturali (tasti diatonici meglio noti come tasti bianchi):

• Do
• Re
• Mi
• Fa
• Sol
• La
• Si

e 5 note alterate (tasti cromatici, meglio noti come tasti neri)

• Do# =  Re♭
• Re#  =  Mi♭
• Fa# =  Sol♭
• Sol# =  La♭
• La# =  Si♭

Ogni ottava è pertanto composta da un totale di 12 diverse note: passando alla 13° nota si salta automaticamente all'ottava successiva. Quella che segue è la sequenza delle note in un'ottava: ogni volta che si va a destra l'altezza del suono aumenta di un semitono.

Do  Do#  Re  Re#  Mi  Fa  Fa#  Sol  Sol#  La  La#  Si

Come possiamo costruire una tabella per le frequenze delle note generate dalla tastiera dell'organo? Seguendo alcune "semplici" regole matematiche:

• per prima cosa dobbiamo fissare un solido punto di riferimento, spesso noto come corista, che è la nota La3 (cioè il La della terza ottava della tastiera) a cui si associa la frequenza di esattamente 440 Hz cioè la frequenza del diapason (si, proprio quella specie di forchettone di metallo che i musicisti non usano per mangiare gli spaghetti ma per accordare gli strumenti, che gente strana 😆)

• ad ogni salto di ottava verso destra deve corrispondere un raddoppio della frequenza dell'onda sonora prodotta e ciò deve valere per qualsiasi tasto:

• ad ogni salto di semitono verso destra la frequenza deve essere incrementata moltiplicandola per la radice dodicesima di due:

L'ultima regola che ho appena descritto è in realtà in grado di "generare" anche quella precedente.

Il numero 2 corrisponde al raddoppio di frequenza che si osserva nel salto di ottava: dato che un'ottava è composta da dodici semitoni, ogni salto di singolo semitono deve contribuire per un dodicesimo rispetto a quello di ottava.

Ecco perché salta fuori la radice dodicesima di due: tale radice si può anche scrivere come due elevato alla un dodicesimo, numero che equivale a poco più di 1,059463.

valore del rapporto di frequenze del semitono equabile

Se parto da una qualsiasi nota la cui frequenza acustica sia pari ad f_n e mi sposto di 12 semitoni verso destra (cioè compio un salto di ottava), posso determinare la frequenza finale moltiplicando la frequenza iniziale per il rapporto di semitono equabile per dodici volte consecutive:

Esempio: voglio determinare la frequenza della nota Mi4 sapendo che la frequenza del corista La3 è 440 Hz.

Sulla tastiera per andare dal La3 al Mi4 devo fare 7 salti di semitono verso destra. Quindi abbiamo:

Inserendo in un programma di fogli di calcolo le formule sopra riportate si ottengono finalmente le frequenze (in Hz) dei 54 tasti. I valori sono leggibili nella terza e ultima colonna della tabella che riporto qui di seguito, mentre la prima colonna riporta il numero progressivo del tasto e la seconda colonna riporta il nome della nota.